In the midst of these huge modifications and upgrades to the game to get the game ready for feature lock, fixing the tail has become a lower priority task. But, last night, I stepped Zac through the tail code, explaining a lot of the how's and the why's of the algorithm. It proved to be very valuable, so I'm going to do the same in this post. Specifically, I will focus on the section of the algorithm that deals with the dragon bouncing off the bounds of the world (a circle).
Before we start, I'd like to note a couple things. The tail is broken up into individual node structures, each doubly linked with a parent node and a child node. This structure is contained in the DragonHead class. I have already explained in my previous post how the dragon's head acts as the managing class for the tail, so I won't go into that here.
The Reflect Component of the Algorithm
Let's start with the simplest part: the physical reflection. It is one line of code:
This line of code simply reflects the node off the wall, in the exact opposite way it was facing (without inverting the head's up vector like it used to).
Now, we'll go in-order in code with what happens when the head first hits the wall. The head hits the wall and calls that Reflect() function on itself; the rigidbody also accounts for this reflection.
The head then tells its child (the first tail node behind the head) that it has reflected. It's functionality is described in the comments.
Without worrying about the math here, the crux of this function is to calculate the time it will take the current node to reach its parent's reflect position given its current velocity. Then, given this reflectionTFinal, the node knows when to reflect itself. A new gameobject with the same transform and velocity as the parent is created, and the node follows that transform for the given time in the same way it would follow its real parent.
This is inherently wrong, as the velocity changes due to an acceleration (via rotation), if the parent was not moving perfectly straight at the time of collision. I will address this later. A funny tidbit about this function: when Zac came over we got to this and I was calculating the distance with a standard distance check using Pythagorean distance. But, after changing it to a Vector3.Distance call from Unity's Vector3 library, we saw a significant increase in reflection stability. We were baffled by this: how could this very rudimentary calculation be wrong?? A little while later we realized that, through a slight oversight, I was square rooting the square distance... twice. Of course, though, that was only one factor of why the tail breaks apart so often.
Let's take a look at how the problem here manifests itself in the game:
The first thing I notice here is that the head is the source of the problem. A side effect of how the tail is written is that it corrects itself over time, especially when the dragon moves in circles without hitting the boundary. The head being the source of the problem makes my proposed solution that much more likely to resolve at least most of the tail bugs.
Let's focus on JUST the dragon head and the node behind it, as the dragon head controls rotations and the node behind it is the most screwed up.
This works great, but only when the head is not turning at any point in time between the reflection of the head and the reflection of the child tail node. Since most of the game is spent turning, this simple position derivative will not work for changing velocities.
It just creates a copy of the parent node, and makes that transform continue forward until the child reflects. During this time period, the child node does it's usual "RotateTowards" behavior on the head copy. At which point, the parent node copy switches parents back to the real head, and destroys the copy.
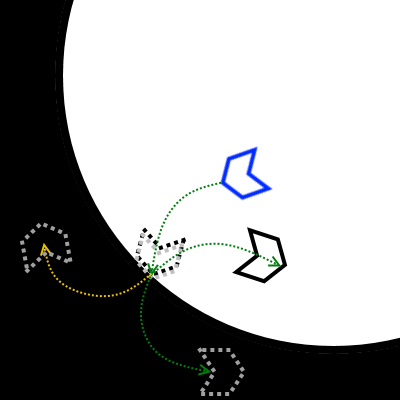
So, my conclusion is that the parent node copy must account for changes in rotation and velocity due to actual parent node turning. There are a few ways to do this, but first let's look at a diagram of what this will look like when rotations are accounted for. Compare the transforms of this diagram with those of the above diagram and it should become apparent why the latter should theoretically work:
The idea here is simple: Just continue the trajectory as if the head had never hit the wall. This is where we'll have to test and see what happens. The gold trajectory is where I predict the correct final position of the head to be, but the green trajectory is also possible.
Alternatively, if this slightly more elegant solution doesn't work, I have another. Instead of even creating a copy of the head:
1) Save off the position of the head at the impact point.
1.5) For testing, save off the rotation of the parent at the time of impact as a unit vector. We can use this to check against the actual unit vector of the reflection of the child.
2) Every physics step, obtain a vector from the collision point to the position of the actual head, NOT normalized.
3) Subtract this vector from the reflect position we defined in step 1.
4) We now have the position the dragon head would have been if it hadn't reflected (the gold dotted line)
One problem I haven't completely worked out with these methods is recalculating the time it will take for the child to reach the parent reflect position. Currently, it derives this time from a linear distance, but, as you can see, the distance is not linear. I need to measure the length of that curve. That cannot be one calculation, though, due to the case that the player stops or starts rotating during that time period. So, like the updating position, that time variable will also need to be updated according to the trajectory of the parent node.
This line of code simply reflects the node off the wall, in the exact opposite way it was facing (without inverting the head's up vector like it used to).
Now, we'll go in-order in code with what happens when the head first hits the wall. The head hits the wall and calls that Reflect() function on itself; the rigidbody also accounts for this reflection.
The head then tells its child (the first tail node behind the head) that it has reflected. It's functionality is described in the comments.
Without worrying about the math here, the crux of this function is to calculate the time it will take the current node to reach its parent's reflect position given its current velocity. Then, given this reflectionTFinal, the node knows when to reflect itself. A new gameobject with the same transform and velocity as the parent is created, and the node follows that transform for the given time in the same way it would follow its real parent.
The Problem
Let's take a look at how the problem here manifests itself in the game:
The first thing I notice here is that the head is the source of the problem. A side effect of how the tail is written is that it corrects itself over time, especially when the dragon moves in circles without hitting the boundary. The head being the source of the problem makes my proposed solution that much more likely to resolve at least most of the tail bugs.
Let's focus on JUST the dragon head and the node behind it, as the dragon head controls rotations and the node behind it is the most screwed up.
This works great, but only when the head is not turning at any point in time between the reflection of the head and the reflection of the child tail node. Since most of the game is spent turning, this simple position derivative will not work for changing velocities.
It just creates a copy of the parent node, and makes that transform continue forward until the child reflects. During this time period, the child node does it's usual "RotateTowards" behavior on the head copy. At which point, the parent node copy switches parents back to the real head, and destroys the copy.
The Conclusion
The idea here is simple: Just continue the trajectory as if the head had never hit the wall. This is where we'll have to test and see what happens. The gold trajectory is where I predict the correct final position of the head to be, but the green trajectory is also possible.
The Code Solution to the Conclusion
Theoretically, if in every physics step I set the head copy's trajectory equal to the inverse of the real head, it should work. The child node will reach the point of collision under the EXACT same conditions (with the correct rotation and velocity) that the head experienced when it reflected. As such, the child should reflect in the EXACT same manner as the head did, and the reflection should be successful.Alternatively, if this slightly more elegant solution doesn't work, I have another. Instead of even creating a copy of the head:
1) Save off the position of the head at the impact point.
1.5) For testing, save off the rotation of the parent at the time of impact as a unit vector. We can use this to check against the actual unit vector of the reflection of the child.
2) Every physics step, obtain a vector from the collision point to the position of the actual head, NOT normalized.
3) Subtract this vector from the reflect position we defined in step 1.
4) We now have the position the dragon head would have been if it hadn't reflected (the gold dotted line)
One problem I haven't completely worked out with these methods is recalculating the time it will take for the child to reach the parent reflect position. Currently, it derives this time from a linear distance, but, as you can see, the distance is not linear. I need to measure the length of that curve. That cannot be one calculation, though, due to the case that the player stops or starts rotating during that time period. So, like the updating position, that time variable will also need to be updated according to the trajectory of the parent node.




No comments:
Post a Comment